Originally posted on Medium.
For a high-level talk on this topic check out the NonTrivial Podcast.
Mathematics as Rigor
Our worldviews are largely based on how we think things work. Our experiences settle into ideas, and we use those ideas to make decisions. Our perceptions don’t exist merely as isolated concepts, rather we fashion them into narratives. A narrative is a story that lays out a causal explanation for the things we experience. For the most part, these explanations reside in us as emotions that rise up whenever we face familiar situations.
But sometimes we need to be rigorous with our explanations. To be rigorous is to be thorough; to exhaust how we choose to argue about how things work. Rigor admits the fewest assumptions, and lays down only what we believe to be absolutely true. A rigorous explanation is ideally robust to interpretation, making such commentary the ultimate goal in science and engineering.
The way we try to be rigorous with our explanations is via precision. Precision is where we strip away the externalities of the messy world and instead anchor our ideas on some set of irrefutable facts. Facts are much harder to dispute than some account of how we feel about a situation.
Of course even lies can be told with a set of facts, merely by rearranging truths into a story that abuses our human dependence on causality. People see patterns, and we can always arrange facts into stories that makes sense, regardless of any genuine connection to reality.
This is why mathematics and rigor have gone hand-in-hand for centuries. Mathematics does not allow all stories to be told. The isolated concepts we believe to be true can only be strung together in accordance with the internal consistency of the mathematical language. By forcing precisely defined concepts into an equally precise set of rules, the machinery of mathematics guarantees the logical outputs we produce.
When we convert our ideas into mathematical form we create the most precise, symbolic version of the mechanisms we believe drive the things we observe and measure. Equating mathematics to rigor is what drives consensus in much of science and engineering. There is an unspoken rule that says any human endeavour that reaches a good level of understanding will be mathematical in nature. No matter the field of study, only when their leading theories have been solidified into the language of mathematics are they to be considered authoritative.
The Cost of Precision
Mathematics is about creating symbols that represent some notion in abstract terms. Symbols for equality =, greater than >, pi π, a function f (x), etc. are all labels that mean something specific. When we look upon those symbols there should be little to no dispute about what they represent.
Think about the idea of a function. A function is something that converts inputs to outputs; like a box that transforms information by doing something in the middle. But such a hand-wavy definition would not suffice in mathematics. There can be no room for misinterpreting what we mean when we say “function.” We must rigorously define a function by saying a function assigns elements from a set X to a set Y such that each element of X exactly maps to one element of Y. That is what a function, f (x), means precisely. With such a clear-cut definition in hand we are free to use it as a symbol, along with other precisely defined symbols, and combine these into the kind of indisputable stories rigor depends on.
But precision is not the same as accuracy. Accuracy is about how close our measurement is to the true value, whereas precision refers to how refined our measurement is. Figure 1 shows the usual way to visualize the difference between accuracy and precision. The closer we are to the centre of the bullseye the more accurate our measurement is (closer to the true value). The tighter our measurements are (how similar our measurements are to each other) the more precise we are.
Figure 1 Visual depiction of the difference between accuracy and precision. Adapted from https://en.wikipedia.org/wiki/Accuracy_and_precision
But if that was the whole story then we could achieve both high precision and high accuracy, as in the following figure:
Figure 2 Visual depiction of achieving both high accuracy and high precision.
Compare measuring something like temperature to the absurd story about measuring intelligence. Even if there was a shred of legitimacy to measuring intelligence it would be just that; a shred of some underlying reality. We can choose to be as precise as we want in our arguments about intelligence, but this has little to do with a genuine connection to reality.
The symbols used in mathematics have been stripped of context to make them strictly defined. If context were to be added to those symbols we could easily find them entirely inappropriate for the system at hand.
Consider a dictionary. A dictionary does not contain the meaning of words, only their definitions. A definition uses words to describe the label we look at, but meaning is what the label actually is in a given situation. The only way to know the meaning of a word is to see how the word is used with other words, such as being embedded in a paragraph or someone’s speech. Those other words that accompany the word of interest provide the context. Context really is everything, and if you remove it you are losing the connection a label or symbol has to reality.
The precise symbols in mathematics only get their meaning by virtue of being embedded in some real life situation. The symbols were arrived at by individuals toiling away, immersed in some messy reality, as they wrestled to figure out some underlying mechanism behind what they experienced.
The cost of precision is that we must remove the very thing that makes something realistic; context. Precision is by definition unreal. This is of course the power of precision. By being unreal, precision creates a sterile version of our ideas, unblemished by the messy details of reality. The stripped-down version of our measurement, model or explanation makes it far less prone to misinterpretation. But precision also means our measurement, model or explanation exists in isolation. A so-called “rigorous” explanation only achieves its cleanliness by removing the very things it purports to explain.
Intuition is More Rigorous
Contrast the precision of mathematics to intuition¹. Intuition is the ability to comprehend something immediately, without the need for explicit definitions or analyses. Intuition must capture context since it doesn’t use labels to define a situation. Intuition operates in some high-dimensional space that provides the genuine meaning of a situation.
What differentiates intuition from other forms of knowledge acquisition is its lack of conscious reasoning. Intuition is an emotional thing; we feel the truth about something rather than being able to articulate it with words. It’s our minds tapping into the essence of what’s happening.
We are brought up in society to view intuition as being a weak or less rigorous notion of truth. As though intuition is merely the starting point to something more true; a catalyst to deeper and more reasoned thought. We are often told, explicitly or implicitly, to not listen to our feelings and to instead pay attention to the data. Data and facts are supposed to cut through our built-in biases, and reveal what is really going on.
But facts are true only in the narrowest sense. As with words in a dictionary, facts mean nothing without context. Again, even lies can be told with facts, by rearranging truths into a false story.
The lack of articulation associated with intuition is not less true; quite the opposite. It’s a comprehension unstripped by precision. Intuition has evolved for millions of years; it is a biological reaction to information in our environment. Intuition must have a greater connection to our underlying reality, since we could not function in complex environments if we needed to articulate precisely what was happening at any given moment.
What should be considered truly rigorous is how connected our measurement, model or explanation is to reality. This is what people take “rigorous” to mean. That’s why rigorous explanations are given such weight in science an engineering. Unfortunately this weight has been assigned largely to mathematics due to not appreciating the cost of precision. This causes readers to suppose rigor at face value. Mathematics gives a good deal of authors a kind of free pass, as few are are willing to challenge the appropriateness of mathematics beyond its own internal consistency.
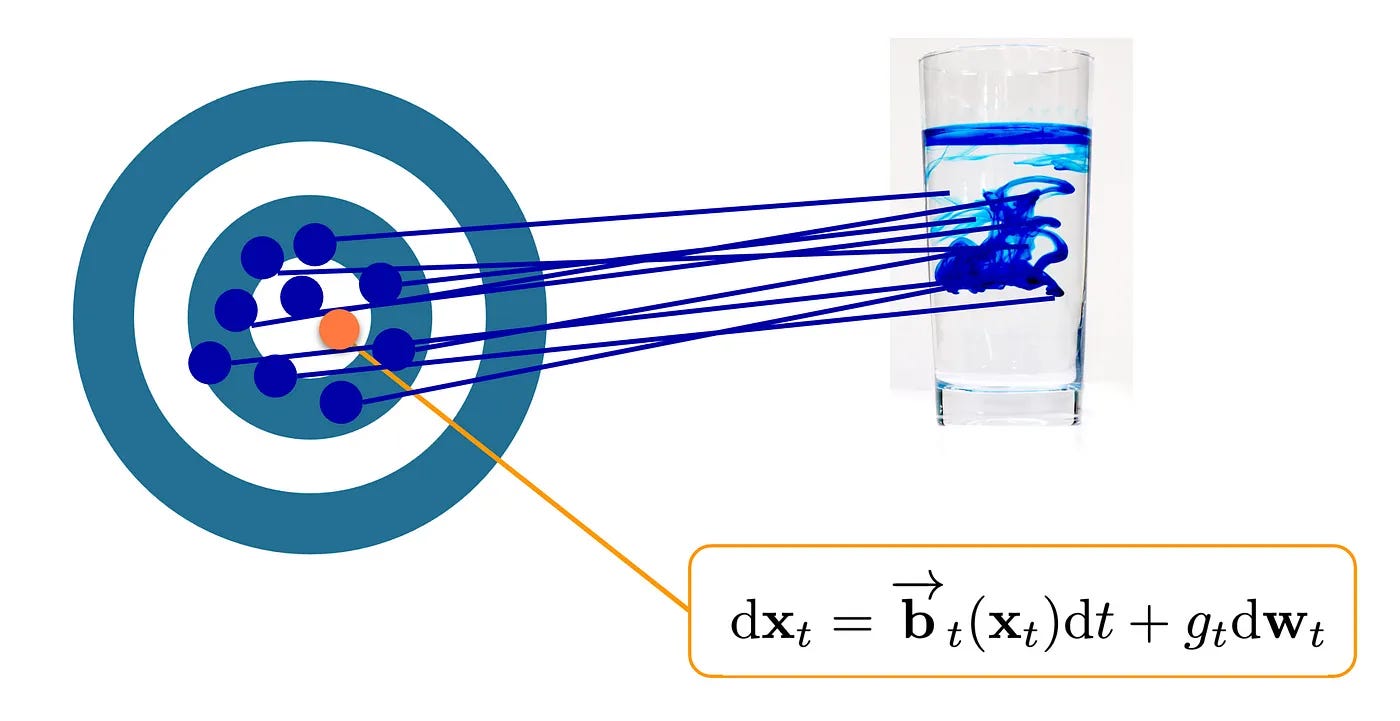
While mathematics restricts the kinds of stories we can tell, this does nothing to guarantee such restrictions map to reality. The restraints imposed on intuition by mathematical machinery can only be accurate in a sparse sense, whereby a few precisely-defined constructs hover above the bullseye of reality, as depicted in Figure 3. Mathematics can have only a slice of accuracy due to its mandatory removal of context through precision.
Figure 3 Depiction of a complex reality, only partially captured by mathematics. Image by author. Ink in glass photograph by Chaozzy Lin.
But this does not negate the cost of precision. Being precisely abstract is still precise. Good mathematics is a collection of abstract symbols born out of context-rich intuition. But only the author of the math used to model a given phenomenon has the original context. They were the ones who bore witness to the ineffable truth imprinted on them in their attempts to understand. This context cannot be communicated through math. The language of mathematics must let go of the rich reality impressed on someone by their intuitions.
Consider how mathematics has been taught through the ages; something most people rightfully despise. We are presented with sterile, meaningless symbols and equations (remember the dictionary) entirely devoid of context. Those who discovered the equations had deep experiences that cannot be described; experiences that have been compressed, sterilized and ripped out of their natural habitats to serve as “education” for the masses.
Mathematics cannot be the most rigorous of depictions because it lacks almost everything that made something recognizable. It captures some irrefutable mechanism, but at the cost of almost everything that makes something real. Abstraction turned into explicit symbolism cannot reclaim the nature that inspired it. The cost is absolute.
Intuition’s Structure
Without story we fail to comprehend much of anything. Humans require precisely defined abstractions to help us navigate the messy details of our world. This is why even if we welcome the idea that intuition is more rigorous than mathematics, it’s hard to accept this at face value. A formal definition of intuition would seem in order.
But isn’t it hypocritical to first argue about the cost of precision relative to intuition, and then suggest we could benefit from a more precise definition of intuition?
Such circularities are avoided as long as we can formalize our ideas without losing context. If we choose a formal framework that exists “outside” the system we are commenting on, it becomes possible to bring precision without disconnecting ourselves from reality.
One of the best examples of this approach is how the logician Kurt Gödel was able to showcase the limitations of mathematics by using metamathematics. Metamathematics is about math, it is not math itself. It would make no sense if Gödel used math to show the limitations of math; this would be akin to arguing God must be true because the Bible says so. Meta is how we avoid the circularity.
I will choose category theory as a type of metamathematics. Category theory is not math, it is about math. It was created to bring together disparate areas of mathematics by finding more fundamental similarities between them. Category theory is now considered a leading framework for the foundation of all mathematics, and can be applied to any area of study that looks to formalize the connective tissue between domains.
So how can we bring category theory to the problem of formalizing intuition? I have been discussing the power of intuition in terms of its ability to connect to reality, in ways mathematics cannot. A connection suggests structure. There must exist some relational construction between what we feel to be true and the nature of what we’re observing. But what is the structure of intuition?
To start in this direction I suggest that intuition is in fact analogy², or more precisely analogy-making³. We make analogies any time we spot similarities between superficially disparate things. To make an analogy is to sense some shared structure between objects or ideas.
If we accept that intuition is rooted in analogy we are then primed to be more formal in our treatment of intuition, since analogies can be expressed rigorously in terms of categorical structure.
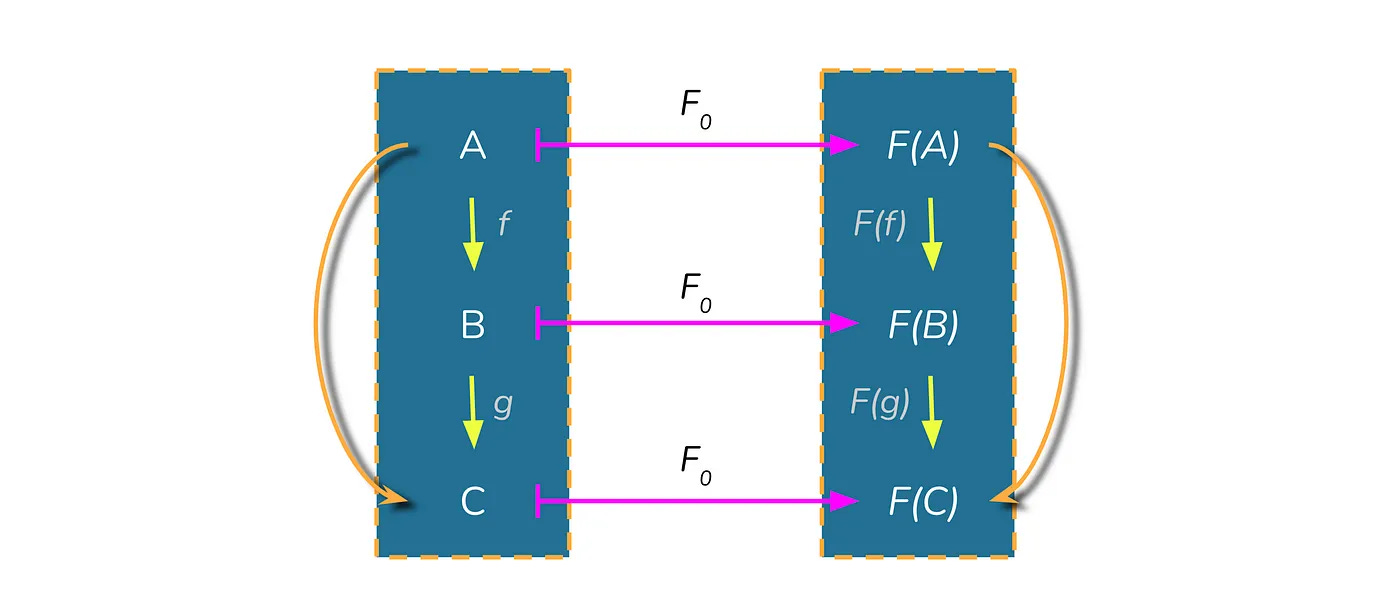
An analogy can be viewed as a structure preserving map between different categories. A formal depiction of this is as follows⁴:
Figure 4 Visual depiction of a Functor from category theory. A functor is a formalization of a structure-preserving map between categories. Image created by author, adapted from reference 4.
A functor can thus be thought of as an isomorphism of categories. An isomorphism is a structure-preserving mapping between two structures that can be reversed by an inverse mapping. It is this preservation of algebraic structure as one moves back-and-forth between said categories that gives us a precisely defined definition of what analogy-making, and thus intuition, is.
If we think about how intuition works in the real world we can see the connection (itself an analogy) between intuition and this isomorphic relation:
any idea exists in our mind as a category, because that’s the only way humans can make sense of the world. We form categories to deal with what would otherwise be sensory overload; and,
to form an analogy is to sense some deeper similarity between ideas.
Bringing this back to the original goal, intuition is the ability to achieve knowledge about something without recourse to conscious reasoning. This could only be achieved if we were making something akin to an isomorphic connection between categories in our mind.
Think about hiring someone for a job. We have categories in our mind related to what defines the job. We also begin to categorize applicants based on their resume and our conversations with them. The decision to hire someone into the company is hardly analytical in nature. Sure, we assess the facts, but ultimately we get a feeling about someone. That feeling arises out of some sense of shared structure between the 2 categories that define our situation.
Every situation in life demands that we form connections between the categories of our current knowledge and the things we are exposed to. We must be creating maps between these categories that have some shared structure, and it is the recognition of such that I argue constitutes intuition.
More context can be seen here as more “lines” that preserve the internal structures between the categories we create in our minds. We can now see, more formally, what it is that precision loses when we choose to capture something symbolically, as we do with mathematics. The lines that define the isomorphic connections of our intuition are being degraded/removed through the necessary act of stripping context.
Letting Intuition Lead
Math is an important aspect of how we go about explaining things. Math has given us the ability to state things unequivocally, which helps land science on some ultimate current state that can be updated as needed. Perhaps best of all is the ability to take what is expressed in mathematics and convert it into computer code, allowing our models to reveal unforeseen patterns as they approach infinity.
But it is not math that we are really after, it is our connection to reality, and it is intuition that contains that connection. Evolution would not endow us with intuition if it weren’t critically connected to our environments.
What we gain from precision we lose in context. Of course we know that all models are wrong, but it’s not simply because they are imperfect reflections of reality. Our models are precise arguments made with symbols and labels, and those constructs are by definition structurally sparse. Precision will always be inadequate when it comes to capturing what is really happening.
This means that we must let intuition lead. An inability to articulate what we feel is not an excuse to bypass emotions for the sake of avoiding misinterpretation. Our intuitions will lead us to profound insights; insights that we can indeed anchor in beautiful mathematics. As long we keep in mind that it is not the math that truly speaks to reality. It is something far more rigorous; the original intuitions that started it all.
When we look upon a mathematical description of something we are looking at how someone chose to anchor their intuitions. We are not looking at some “language of nature” as though low-dimensional symbolism speaks to nature’s true machinery. Mathematics is a story, one that grasps nature at a glancing angle.
I think the current paradigm of science and engineering forgets this, and sees mathematics as the ultimate end goal. Math is not the end goal, it never can be. It is our intuitions that hold the truth of any situation. It is our intuitions that we are chasing. Math must serve those, not the other way around.
We should never let conscious reasoning supersede our natural ability to connect to what is real. It is the connection that matters. It is that fantastically intricate internal structure that somehow remains untouched between ideas and observations.
Intuition must always have the last say.
See my tweet here.